Overview
Any 2 locations on a map will have a distance and a bearing between the 2 points.

If you must travel due East to get from A to B, your bearing would be 90 degrees. If you were traveling due west your bearing would be 270 degrees.
There are different ways to specify position on a map. Latitude and Longitude are commonly used, but one problem with Lat/Long is the distances between Lat/Long positions is not easily calculated using Lat/Long and it also makes it hard to calculate surface areas.
UTM Coordinates
UTM coordinates are one answer to the Lat/Long problem. UTM coordinates make a grid of the map which is measured in meters.
With a map using UTM you can easily measure and plot positions.
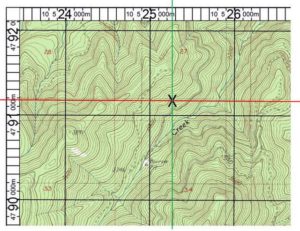
There are lots of great discussions of UTM on the internet – here is one – https://sectionhiker.com/the-universal-transverse-mercator-utm-grid-system-by-blake-miller/
Calculating Bearing
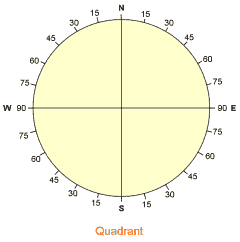
The challenge to calculating a bearing is you must first determine the quadrant that the “to” point is located in; NE, SE, SW, or NW. Once that is determined the calculation of bearing is relatively easy and can be done with some simple trigonometry – which is part of your assignment.
Video
Additional Calculation Information
Here is some additional information about understanding the 4 quadrants of the compass rose.
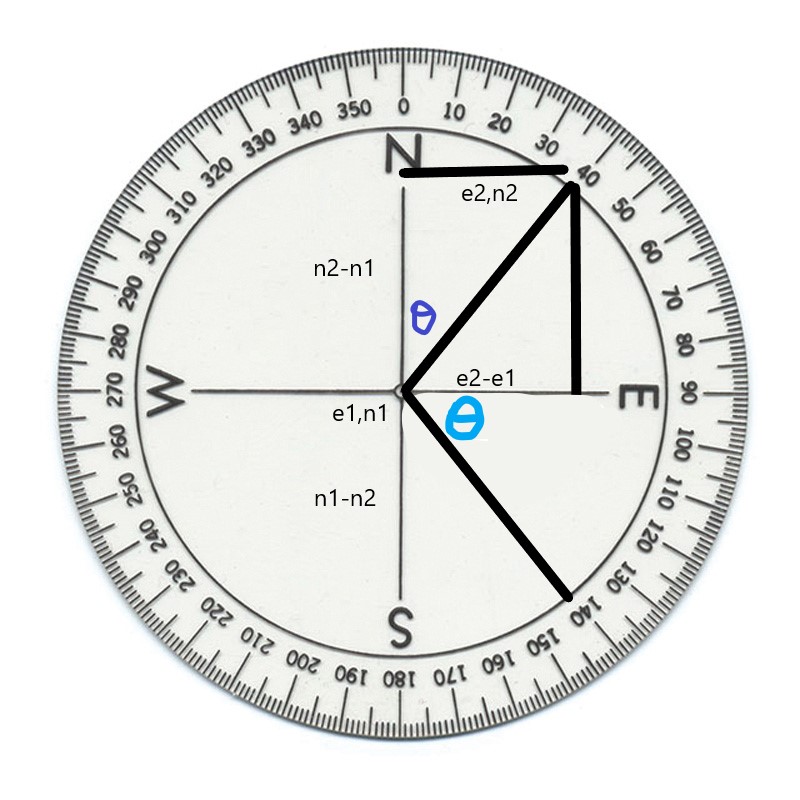
Looking at this compass rose we can see that if a point falls in the NE quadrant then the calculation of the angle (bearing) is pretty easy. if e1, and n1 are the center, then the NE quadrant is defined as n2>n1 and e2>e1. The tangent of the angle is the opposite/adjacent. The length of the opposite is e2-e1 and the length of the adjacent is n2-n1. So this makes for a pretty easy calcuation.
The SE quadrant is a little more difficult, and is defined as e2>e1 and n1>n2. The angle is measures from the right angle or 90 degree bearing line. The same calculation applies but the distances are a little different with the opposite length being n1-n2 and the adjacent is still e2-e1. We must add 90 to the calculated angle to get the bearing.
This process is repeated for all 4 quadrants, so when we want to calculate bearing we must first (1) determine the quadrant, (2) use the correct distances to calculate the angle, and (3) add the correct amount to the angle to get the bearing.