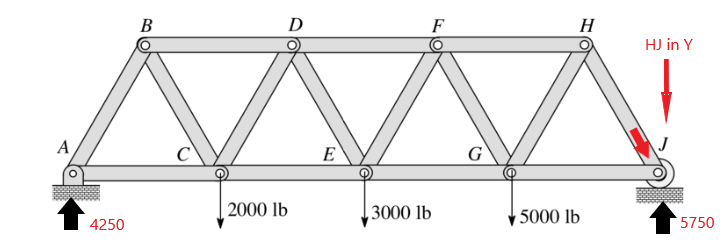
After solving for the resultant forces at the ends we can get the following resultant forces. Please note compression and tension forces.
The first step is a simple sum of moments around A which gives;
(-2000)(1) + (-3000)(2) + (-5000)(3) + FJ(4) = 0
FJ = 5750
From there we can sum all forces in the Y and find the FA = 4250
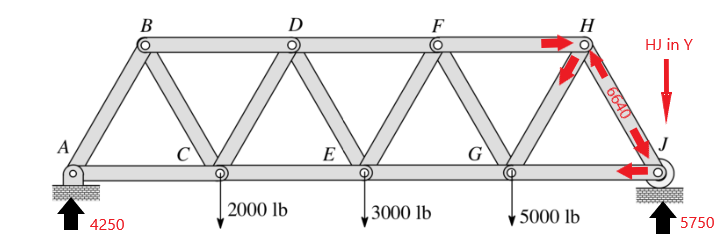
Now we will progress through the truss solving for each member. We can start with the Force of HJ at J, summing forces at J in the Y gives
5750 – F(HJ) cos(30) = 0
F(HJ) = 6639.528 lb (displayed as 6640)
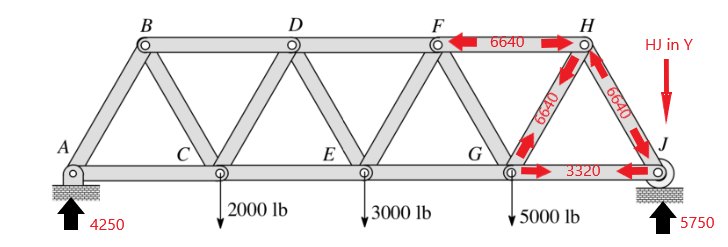
Knowing the Force vector at HG we now have enough information to calculate 2 more
Sum Forces at H in Y
6639.528 cos(30) – F(GH) cos(30) = 0
F(GH) = 6639.528 lb
Sum Forces at H in X
-6639.528sin(30) – F(GH) sin(30) + F(FH) = 0
F(FH) = 6639.528 lb
Sum Forces at J in X
6639.528sin(30) – F(GJ) = 0
F(GJ) = 3319.764 lb
Next Step is to Sum the Forces at G in the Y (which adds the first external force)
F(GH)cos(30) – 5000 + F(GF)cos(30) = 0
F(GF)cos(30) = -750
F(GF) = -866.025 lb or 866.025 lb tension
This allows us to Sum Forces in X at G
F(FG)cos(60) + 6640cos(60) + 3320 – F(EG) = 0
F(EG) = 7072.54 lb (compression)
Sum Forces at F in the Y
F(FE) = 866.025 (compression)
Sum Forces at F in X
F(DF) = 7505.553 lb
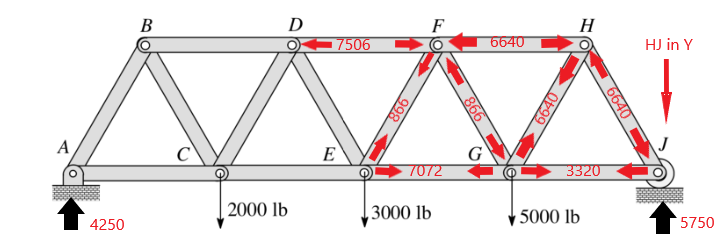
We can progress
Sum Forces at E in Y gives F(DE) = 2598.076 lb (compression)
Sum Forces at E in X gives
F(CE) = 7072.54 + 433.013 – 1299.038 = 6206.515 lb (compression)
Continuing through the entire system gives the following (we left BD, AC, abd BD as an exercise for the students.
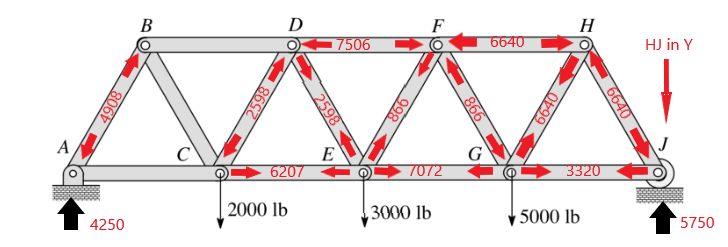
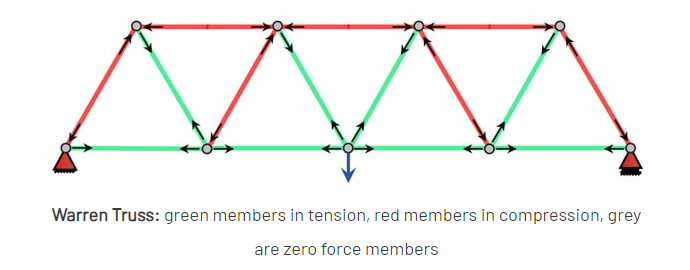
Let’s next compare this to how a center loaded truss would look (I’ll give this one to you). The same pattern of compression and tension members is in the example given for you to solve.