Assignment 5 – Find Depth of Flow in an Open Channel
Outcome
Use an iterative numerical technique to calculate a value
Assignment
The Mannings Equation is used to find the Flow Q (cubic feet per second or cfs) in an open channel. The equation is
Q = 1.49/n * A * R^2/3 * S^1/2
Where
Q = Flowrate in cfs
A = Cross Sectional Area of Flow (square feet)
R = Hydraulic Radius (A/ Wetted Perimeter )
S = Downward Slope of the Channel (fraction)
The Wetted Perimeter and the Cross-Section of Flow are both dependent on the geometry of the channel. For this assignment we are going to use a Trapezoidal Channel.
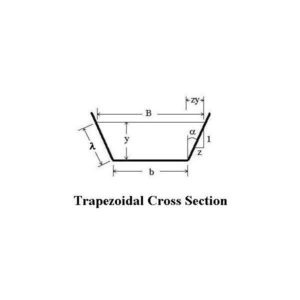
If you work out the Flow Area you will find it is
A = b*y + y*(z*y) = by + z*y^2
The Wetted Perimeter is a little trickier but a little geometry will show it to be
W = b + 2y(1 + z^2)^1/2
where b = base width (ft); z = Side slope; y = depth.
Putting it all together gives a Hydraulic Radius of
R = (b*y + z*y^2)/(b + 2y*(1+z^2))^1/2
All this goes into the Mannings Equations
Q = 1/49/n * (b*y + z*y^2) * ((b*y + z*y^2)/(b + 2y(1+z^2))^1/2)^2/3 * S^1/2
Luckily I will give you the code for this equation in Python. You are free to use this code. Please note that YOU will be solving for y (depth in this function) using iterative techniques.
def TrapezoidalQ(n,b,y,z,s): # n is Manning's n - table at # https://www.engineeringtoolbox.com/mannings-roughness-d_799.html # b = Bottom width of channel (ft) # y = Depth of channel (ft) # z = Side slope of channel (horizontal) # s = Directional slope of channel - direction of flow A = b*y + z*y*y W = b + 2*y*math.sqrt(1 + z*z) R = A/W Q = 1.49/n * A * math.pow(R, 2.0/3.0) * math.sqrt(s) return Q |
As an engineer you are designing a warning system that must trigger when the flow is 50 cfs, but your measuring systems measures depth. What will be the depth where you trigger the alarm?
The values to use
Manning’s n -Earth Channel – Clean
b = 3 foot bottom
z = 2 Horiz : 1 Vert Side Slope
s = 1 foot drop for every 100 feet
(hint: A depth of 1 foot will give you Q = 25.1 cfs)
Write the program code and create a document that demonstrates you can use the code to solve this problem using iterative techniques.
You should call your function CalculateDepth(Q, n, w, z, s). Inputs should be Q (flow), Manning’s n, Bottom Width, Side Slope, Longitudinal Slope. It should demonstrate an iterative method to converge on a solution with 0.01 foot accuracy.
As always this will be done as an engineering report. Python does include libraries to automatically work on iterative solutions to equations – you will not use these for this assignment (but are welcome to use them in later assignments). You need to (1) figure out the algorithm for iterative solutions, (2) translate that into code, (3) use the code to solve this problem, (4) write a report of using this to solve the problem.
As always use the discussion boards to help you figure this one out. This is challenging both mathematically and on the computer. It may be useful to work out the solution by hand (trial and error) to better understand the iterative solution.
Here is a little help that can be used to easily look at the answers. Plotting Used For Checking – Flow problem
Materials
Lecture 5 (Iterative Solution Function)- https://youtu.be/JrIIb1-tczY
Lecture 5 Using Recursion – https://youtu.be/0qpJrRlBm1Y – There are multiple techniques to solve this, this is one very commonly accepted programming technique called recursion.
Lecture (Doing an iterative solution by hand) – https://youtu.be/jvTThe4HWrQ
I even made a second video of doing it by hand. Please don’t tell me you are lost unless you watch these – https://www.youtube.com/watch?v=gxwQiq4Vt8o
Python Tutorial – https://www.w3schools.com/python/default.asp – You should have now completed the first part of the Python Tutorial from Intro to Conda (replaces PIP). You will start using Conda soon to download packages that you will use in future assignments.
You can read up on iterative techniques at https://en.wikipedia.org/wiki/Iterative_method – I am only interested in you coming up with one that works.
This will be handy – you can check your answers with this online version – http://onlinecalc.sdsu.edu/onlinechannel01.php
More than likely you will use a method like Newton Raphson https://en.wikipedia.org/wiki/Newton%27s_method , Bisection Method https://en.wikipedia.org/wiki/Bisection_method or Euler’s Method https://en.wikipedia.org/wiki/Euler_method
