Assignment 6 – Arrays and Matrices
Objective
Use matrix methods to solve engineering problems using Python and Numpy
Assignment
Here is the classic case truss example.
You will be solving for the maximum compression and tension Force on one of the members of the truss. The truss problem you will solve is linked here.
Below is an example of a truss problem that you can use to help you do the calculations for the problem you will complete. This is NOT the truss to solve for the problem. It is an example you can use to figure out how to solve this. You CAN discuss approaches freely on the discussion boards.
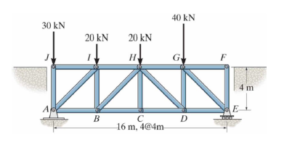
The upward forces at A can be calculated by taking a summation of the moments at E
Moment is distance * force
Moment at E = 0 = 40*4 + 20*8 + 20*12 + 30*16 – FA * 16
FA = 65 kN
Similarly FE = 45 kN
With this information we can do Sum of Forces in X and Y at each node to generate the matrix
Members (17): AJ, AI, AB, BI, BH, BC, CH, CD, DH, DG, DE, EG, EF, JI, IH, HG, GF
You will need 17 equations to solve for the forces in each of these members.
Solve this problem using a matrix solution and report the maximum compression member and value and the maximum tension member and value.
Information
The most challenging part will be determining the force vectors which will involve summing the Force in X and Force in Y at the joints.
https://youtu.be/83W2SQSIXqY – Youtube video of solving the Classic Truss problem.
You may freely write the Summation of Force Equations for the members and discuss these equations. You will not need to use all available equations (Sum forces and sum of moments) to solve for all the force members. You must write your own program to solve the problem which will involve using the geometries to set up the matrix and Python and Numpy to solve the matrix for the forces.
If you are having trouble figuring out how to write the force equations, the discussion board is a great place to ask questions. Everyone should be familiar with at least basic matrix algebra based on the pre-requisites of the course.
This will be a relatively complex engineering report as there are lots of results to report and a complex methodology. I recommend discussing approaches to do this on the discussion boards.
Additional Help
Since you will be working with a large matrix – it is sometimes easier to edit the matrix by itself as a text file in csv format. Excel is also good and can save files as a csv (or comma delimted). My csv file looks something like this;
-1,0,-0.707, 0, 0, 0, 0,0, 0, 0, 0,0, 0, 0, 0, 0, 0
0, 0,-0.707, 0,-1, 0, 0,0, 0, 0, 0,0, 0, 0, 0, 0, 0
0, 0, 0.707, 1, 0, 0, 0,0, 0, 0, 0,0, 0, 0, 0, 0, 0
0, 1, 0.707, 0, 0, 0,-1,0, 0, 0, 0,0, 0, 0, 0, 0, 0
0, 0, 0,-1, 0,-0.707, 0,0, 0, 0, 0,0, 0, 0, 0, 0, 0
0, 0, 0, 0, 1,-0.707, 0,0,-1, 0, 0,0, 0, 0, 0, 0, 0
0, 0, 0, 0, 0, 0.707, 0,1, 0, 0,-0.707,0, 0, 0, 0, 0, 0
0, 0, 0, 0, 0, 0.707, 1,0, 0,-1,-0.707,0, 0, 0, 0, 0, 0
0, 0, 0, 0, 0, 0, 0,0, 0, 0,-0.707,0, 0,-1, 0, 0, 0
0, 0, 0, 0, 0, 0, 0,0, 0, 0, 0.707,1,-1, 0, 0, 0, 0
0, 0, 0, 0, 0, 0, 0,0, 0, 0, 0,0, 0, 0,-0.707, 0,-1
0, 0, 0, 0, 0, 0, 0,0, 0, 0, 0,0, 1, 0, 0.707, 0, 0
0, 0, 0, 0, 0, 0, 0,0, 0, 0, 0,0, 0, 1, 0.707, 0, 0
0, 0, 0, 0, 0, 0, 0,0, 0, 1, 0,0, 0, 0,-0.707,-1, 0
0, 0, 0, 0, 0, 0, 0,0, 0, 0, 0,0, 0, 0, 0, 0,-1
0, 0, 0, 0, 0, 0, 0,0, 0, 0, 0,0, 0, 0, 0, 1, 0
1, 0, 0, 0, 0, 0, 0,0, 0, 0, 0,0, 0, 0, 0, 0, 0
Of course – if you do this you will need to be able to read this into the program as a matrix – so here is some code using the pandas library to make that easy.
Note: You cannot simply copy and paste this into your code, this is specifically the order and assumptions I made when solve the problem and the columns correspond with nodes that must correspond with the other 2 arrays.
import pandas
"We will use the pandas function read_csv to bring the data in as a dataframe"
df = pandas.read_csv(
r"C:\Users\eaglinr\Documents\classes\EGN3214\trussdata2.csv",
sep=",",
dtype=float)
"We need it as a matrix for algebra which can be done with the tolist() function"
values = df.values.tolist()
It is worth looking at the pandas library which does have the ability to directly read from an Excel file (among other formats). If you were to use Excel your table may look like this (note I did NOT label exact nodes and trusses – since that is your job when solving the problem and simply copy and paste of my solution is not solving it yourself.
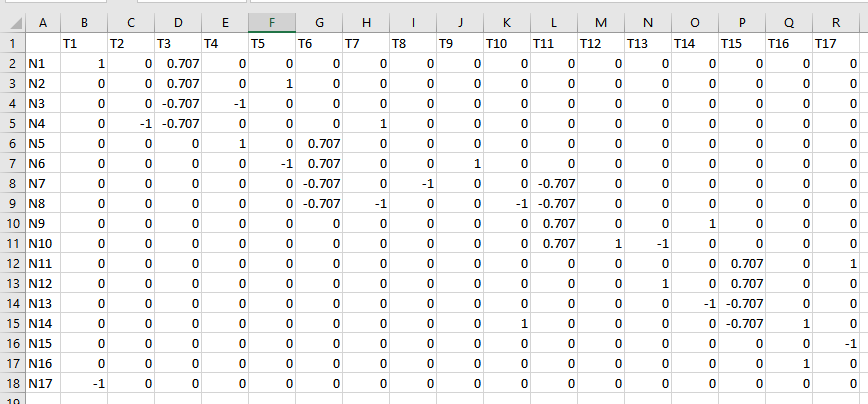
Here is the code to import this, the header specifies the row that has header information, the index_col specifies the column that has title information, dtype is float ensures that the data itself is converted to floats not strings when you convert to a list.
df = pandas.read_excel(
r"C:\Users\eaglinr\Documents\classes\EGN3214\trussdata.xlsx",
header = 0,
index_col = 0,
dtype=float)
values = df.values.tolist()A Little About Matrix Math
Note: If you are weak on matrix math you MUST read and follow this. You will not be able to make it through any engineering curriculum without knowing basic matrix mathematics.
Even though you should have had some matrix algebra in previous classes, I do realize it might have been a while. Here is the basic matrix math you will use to solve this problem. Let’s consider a simple matrix math ;
| 1 -1 2 |
A = | 2 1 -2 |
| -1 2 1 |
B = | 1 -1 2 |
| (1)(1) + (-1)(-1) + (2)(2) | | 6 |
A x B = | (2)(1) + (1)(-1) + (2)(-2) | = | -3 |
| (-1)(1) + (2)(-1) + (1)(2) | | -1 |
The beauty of this is it allows us to solve multiple equations in multiple unknowns. If you change the way around to look like this;
| 1 -1 2 |
A = | 2 1 -2 |
| -1 2 1 |
B = | x y z |
| (1)(x) + (-1)(y) + (2)(z) | | 6 |
A x B = | (2)(x) + (1)(y) + (-2)(z) | = | -3 |
| (-1)(x) + (2)(y) + (1)(z) | | -1 |
We can use matrix methods to solve for x, y, and z (same as solving for matrix B). This is the form A x B = C, we are solving for C so we take the inverse of A and then the result as the dot product of A^-1 dot C. You will find that the code here gives you the original b = [1 -1 2]
a = numpy.array([[1,-1,2], [2, 1, -2], [-1,2,1]])
c = numpy.array([6, -3, -1])
b = numpy.linalg.inv(a).dot(c)The matrix problem you are solving is the same thing only on a larger scale – but that is the beauty of the matrix math, it allows for much larger solutions of n equations in n unknowns.
A Little About Force Vectors
o A
/|
/ |
/ |
/ |
B o----o CLet’s look a little at Force vectors. The diagram above has 3 members; AB, AC, and BC. If we assume all 3 are in compression then (you can assume anything – simply be consistent);
- Fy(AB) at B is negative, Fy(AB) at A is positive
- Fx(AB) at B is negative, Fx(AB) at A is positive
- Fy(BC) is 0
- Fx(AC) is 0
- Fy(AC) at A is positive, Fy(AC) at C is negative,
- Fx(BC) at B is negative, Fx(BC) at C is positive
If there are external forces in this 3 legged truss we can write an equation at each node, put them in a matrix and solve for the compressive forces in each member. It really is that easy – and it scales to much larger problems. It does require a little trig as the force vectors are always in the direction of the member, so the x and y are those components of that vector.
So if you force vector calculates negative – that simply means the member is in tension, not compression. You now have all the basic concepts to solve this and much more complex truss problems (under assumptions the members are not adding forces due to their own weight – which is a huge assumption that you will learn how to handle in Statics class)
Want More?
- Good PDF of the truss problem general solution with code – http://www.unm.edu/~bgreen/ME360/Statics%20-%20Truss%20Problem.pdf
