Topic 10 – The Tree Data Structures
Introduction
Once again we have a data structure (and an Abstract Data Type) that mimics a great real world analogy. The terminology of trees is easy; nodes, branches, root, leaf, parent, child, siblings – all documented at the article at https://en.wikipedia.org/wiki/Tree_%28data_structure%29. You will need to know this terminology, and you will also need to have a solid understanding of trees as we move forward. You will find that this structure is quite useful for many computer science and programming tasks.
Abstract Data Type
Let’s talk about the concept of a tree as an abstract data type, thus meaning it is defined by its interface. This interface would be
Create, Destroy, InsertNode, DeleteNode, RetrieveNode, Traverse, Empty, Full, Count
other methods could also be implemented (such as Sort) but they would be specific to implementations and the use of the Tree.
Implementation of a Tree
A specific implementation of a tree is shown in this Fiddle – https://jsfiddle.net/reaglin/9kbk4jb5/ . The tree shown is a self balancing tree in that nodes are added to the tree and automatically balance from left to right keeping the depth of the tree relatively uniform. This example alone demonstrates that there can be many types of trees (based on implementation details) and rules used for creation of nodes and branches. Different types of trees can be used for many different types of purposes – but the implementation demonstrates one specific type of tree.
Video – Binary Trees
Link – https://www.youtube.com/watch?v=HWnbgEEZq4g
Types of Trees
Trees can be defined by their implementations and the rules used to create, define, or traverse the tree. Because of the many needs and uses of trees – there are many types of different kinds of trees used in programming and computer systems.
Binary Trees
A binary tree is a simple implementation of a tree where a node can have at most 2 branches (or subtrees). Good details about binary trees is at https://en.wikipedia.org/wiki/Binary_tree. Please note a binary tree is NOT a B-Tree. So here is one use of a binary tree – a specific case called an expression tree. An expression tree is a binary tree that can be used to store an algebraic expression. For example a + b * (c + d) can be expressed as the binary tree shown.
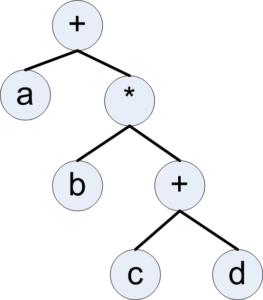
You will need to know how to create and use binary trees, for data storage and also implementation of search algorithms.
AVL Trees
The AVL (Adelson-Velskii) tree is a tree where the heights of the subtrees differs by no more than one. The value of having a balanced tree is that it reduces the complexity of searching the tree from O(n) for a completely unbalanced tree to O(log2n) for a completely balanced tree. Of course this means we would need an algorithm to balance our tree – and as expected wikipeida has excellent discussion of AVL trees – https://en.wikipedia.org/wiki/AVL_tree
Expression Trees
An expression tree is a very common use for a binary tree structure. Expression trees are created specifically to retain and implement algebraic and boolean expressions. More information about binary expression trees is at https://en.wikipedia.org/wiki/Binary_expression_tree
Heap or Heap Tree
A Heap is also a binary tree, in this case with the properties that (1) the Tree is complete or nearly complete, and (2) the key value of each node is greater than or equal to the key value of each of its descendents. More information on a Heap is given here https://en.wikipedia.org/wiki/Heap_%28data_structure%29
Video of Trees
Two video’s for binary trees structures is at All Course Lectures in section 4.1, 4.2, and 4.3.
B-Tree
First a B-Tree is NOT a binary tree (the B stands for Boeing where the team that created them was from). In fact a B-tree can have multiple subtrees. The values in a node in a B-tree are called keys – and their values are important. For example if a node had three values 5, 10, and 20 they would be ordered within the node, like so.
| – | 5 | – | 10 | – | 20 | – |
Now – it is the spaces between the values that are important. Since there are three values, there are 4 spaces – so this tree would have an order of 4. Values are added by creating subtrees. So far all we have is a M-way tree, but by adding a few constraints we make it a B-Tree.
1. The root is either a leaf or it has 2 … m subtrees
2. ALL internal nodes have at least m/2 non-null subtrees
3. ALL internal nodes have at least m non-null subtrees
4. ALL leaf nodes are at the same level.
5. A leaf has at least m/2-1 and at most m-1 entries
You should read the discussion at https://en.wikipedia.org/wiki/B-tree – the most complex things to deal with in B-trees is inserting and deleting nodes and still maintaining all the rules defining a B-Tree. I recommend watching the animation at http://www.csanimated.com/animation.php?t=B-tree – you WILL need to be able to follow this logic and do this.
TRIES
Imagine you are checking the spelling of the word globult (which is not a word). You need an algorithm to check it against the dictionary – so you start with the first letter, since there are plenty of entries in the dictionary starting with g – you move on to the g > l, and so on. All the way to the end g > l > o > b > u > l we still have entries (since globule is a word). When you add that last t, there are no entries – so the spell check fails. As a bonus you do have entries that are close that you can suggest! a TRIE is a tree data structure designed just for such a task. You should review the article at https://en.wikipedia.org/wiki/Trie to be sure you understand how this structure works.
Additional Resources
If you find additional resources that can help you or other students succeed in this course, please post to the discussion boards or email to Dr. Eaglin
